Survivor Contestants Faced This Challenge and They Did Not Do Well

Survivor has produced a whopping 45 seasons, with more in development. If you remember the buzz around season 1 but can’t believe it’s been 45 years, it hasn’t. They’ve cranked out two seasons per year for most of its run to feed their insatiable fanbase. Each season, the mega-successful reality show maroons an attractive cast of clashing personalities on a tropical island to compete for a million dollar prize. Contestants are subjected to physical, endurance, and mental challenges to earn survival gear or immunity from being voted off the show. The island rapidly devolves into a pressure cooker of scheming and backstabbing, much to the viewers’ delight.

This week’s puzzle comes from a real mental challenge that the show used in the season 5 premiere, set in Thailand. Two teams compete in a strategy game, but as you’ll discover, one team can always force a win with the right moves. The castaways failed to find the optimal strategy in real time, instead exchanging blunders until it was too late for one team. This is understandable under time pressure, but some fans have lamented that the existence of an unbeatable strategy made the game unfair.

Let me know if you think you would have cracked this one on a sweltering beach with television cameras in your face. Good luck—your tribe is counting on you.

Did you miss last week’s puzzle? Check it out here, and find its solution at the bottom of today’s article. Be careful not to read too far ahead if you haven’t solved last week’s yet!

Puzzle #30: Survivor Flags

Jeff Probst has planted 21 flags in the ground. Tribe A and Tribe B will alternate removing either one, two, or three flags at a time (zero is not allowed). The tribe that removes the last flag wins. If Tribe A goes first, which team can force a win and what is the winning strategy?

I’ll be back next Monday with the solution and a new puzzle. Do you know a cool puzzle that you think should be featured here? Message me on Twitter @JackPMurtagh or email me at gizmodopuzzle@gmail.com

Solution to Puzzle #29: A Sporting Chance

Did you emerge victorious from last week’s competitive puzzles?

I missed the Super Bowl. All I know is that the two teams were perfectly matched in skill (suspend your disbelief) and that the score was not tied at halftime. I want to know the chances that the team who trailed at halftime pulled a comeback to win the game. Given only this information, what should I put the chances at?

By perfectly matched, I mean that the teams have the same probabilities of achieving various scores and furthermore these probabilities don’t change based on game situation (i.e. which half they’re in or who’s ahead). Remember that Super Bowl games cannot end in ties: if scores are even after the second half, they enter overtime.

The chance that the team who trails at halftime pulls a comeback and wins the game is 25%. Consider each half of the game separately. We’ll ignore all ties because we’re told that the game is not tied at halftime and we know that the game is not allowed to end in a tie. Let’s call the teams A and B and note who “wins” each half, ignoring the other half. There are four possibilities: AA, AB, BA, BB (e.g. BA means that B scores more than A in the first half, but A scores more than B in the second half).

Of course, it’s not only important who wins each half but also by how much. In BA, B could be winning by 40 points in the first half and only have lost the second half by 2 points and would thus still win the whole game. Let’s lay out all possibilities in a table:

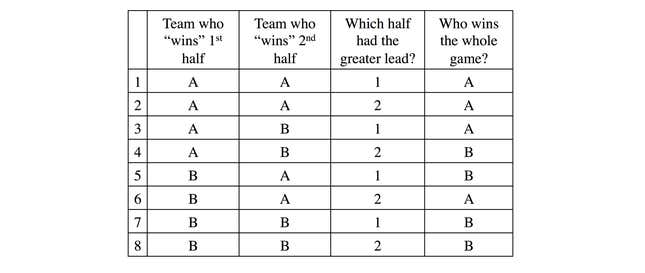
A key insight is that, because the teams are evenly matched, all eight possibilities occur with equal probability. Both teams have a 50/50 chance of scoring more points in either half. And the first half is equally likely to have a bigger or smaller spread than the second half. Only two of the eight rows (25%) signify games where the team who trailed at halftime pulled a comeback: row 4 and row 6. For example, row 5 means that A trailed at halftime and despite scoring more than B in the second half, it wasn’t enough to make up A’s deficit.

Dr. Emilio Lizardo guessed the correct answer of 25% because football broadcasts often quote that number. He shared a link to this article that looks at almost 40 years of NFL games and finds that the team who leads at halftime wins between 73% and 82% of the time. An analysis of NBA games found that 74.8% of the time, the team who leads at halftime goes on to win the game. So this simplified model might be onto something!

Now, on to last week’s bonus puzzle.

Several teams participate in a simple round-robin tournament (i.e. every team plays every other team once). Call a team a super-winner if every other team in the tournament either lost to them or lost to someone who lost to them. Argue that every tournament has at least one super-winner.

Shout-out to Eugenius for a perfectly concise solution to the bonus puzzle.

Look at the team that won the most games. If there are ties, just pick any one of them. Let’s call them The Goats. We picked The Goats because no team won more games than they did. I claim The Goats must be super-winners. Suppose they weren’t super-winners. This assumption will lead to a contradiction, allowing us to conclude that The Goats were in fact super-winners.

If they’re not super-winners, then there must be some team, let’s call them The Underdogs, that beat The Goats and beat everybody who The Goats beat. But this would mean that The Underdogs won more games than The Goats! Because The Underdogs beat every team The Goats beat plus The Goats themselves. Nobody won more games than The Goats, so this is a contradiction and our assumption must have been false: The Goats were in fact super-winners.